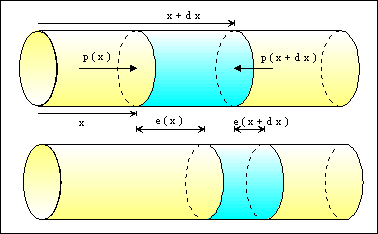
Figura 1. Formarea undei datorita elasticitatii (legea Hooke) si legii fortei.
Intr-un mediu elastic vibratia unui corp se transmite particulelor mediului aflate in contact cu el. Datorita interactiunii elastice dintre particulele mediului aceasta perturbatie nu ramane localizata langa sursa perturbatoare ci se propaga. Particulele puse in miscare de corpul care vibreaza actioneaza asupra particulelor invecinate care la randul lor antreneaza alte particule si asa mai departe. In acest mod se creaza unde elastice in mediu, care se propaga de la sursa initiala in intreg spatiul.
Cum se formeaza o unda
Intr-un cilindru cu sectiunea S, extins de-a lungul axei Ox, delimitam un corp prin doua sectiuni transversale aflate la distanta "x" si respectiv "x+dx" de originea axei. Acest cilindru infinitezimal este deplasat si deformat de catre perturbatia care se propaga prin mediu.

Figura 1. Formarea undei datorita elasticitatii
(legea Hooke) si legii fortei.
Miscarea cilindrului este controlata de legea a doua a dinamicii:
F = m·a (1)
care dupa simplificari devine urmatoarea ecuatie de miscare:
¶ p/¶ x = -r · ¶ v/¶ t (2)
S-a tinut seama ca forta totala care actioneaza asupra corpului este generata de presiunile ce actioneaza pe cele doua baze ale cilindrului:
F = p(x)·S – p(x+dx)·S = –S·dx·¶ p/¶ x (3a)
masa lui este:
m = r ·S·dx (3b)
si acceleratia:
a = ¶ v/¶ t (3c)
Deformarea corpului este descrisa de legea lui Hooke, unde tensiunea mecanica indusa in corp este egala cu forta ce actioneaza pe una din bazele cilindrului, forta de pe a doua baza fiind forta de reactiune:
p = F/S = - E·D L/L (4)
Lungimea initiala a cilindrului este "dx", iar modificarea lungimii lui este data de diferenta dintre cele doua elongatii (deplasari) pe care le sufera cele doua sectiuni:
D L = e(x+dx) – e(x) = (¶ e/¶ x)·dx (5)
Efectuand simplificarile ce se impun obtinem legea lui Hooke de forma urmatoare:
p = - E·(¶ e/¶ x) (6)
unde "E" este modulul de elasticitate longitudinal (Young) al mediului.
Combinand relatia (6) cu relatia (2) obtinem ecuatia undelor pentru acest caz simplu al propagarii unidimensionale:
¶2e/¶ x2 = (1/c2) ¶2e/¶ t2 (7)
unde:
c = (E / r )1/2 (8)
este viteza de propagare a undei. Fiindca viteza de oscilatie este derivata elongatiei v=¶ e/¶ t, obtinem derivand relatia (7) dupa t:
¶2v/¶ x2 = (1/c2) ¶2v/¶ t2. (9)
o ecuatie a undelor pentru viteza. Derivand ecuatia (7) dupa "x", tinand cont de relatia (6) avem :
¶2p/¶ x2 = (1/c2) ¶2p/¶ t2 (10)
tot o ecuatie a undelor pentru presiune.
Solutia generala pentru ecuatia undelor (11) este de tipul:
e(x,t) = f1(x–ct) + f2(x+ct) (11)
lucru care se poate verifica imediat prin derivarea solutiei (11) dupa "x" si "t" si inlocuirea in ecuatia (10). Functiile f1 si f2 sunt arbitrare, forma lor concreta fiind impusa de modul in care se excita mediul. De exemplu daca punem in miscare mediul printr-o excitatie armonica atunci functiile f1 si f2 vor fi functii armonice. Functia f1 descrie propagarea perturbatiei in sensul axei Ox (de la stanga la dreapta pe figura), iar functia f2 descrie propagarea perturbatiei in sens contrar axei Ox (de la dreapta la stanga pe figura).