Figura
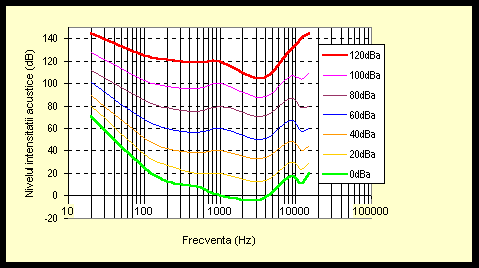
2. Curbele de nivel acustic functie de frecventa.
– Intensitatea sonora (I) = energia acustica care trece prin unitatea de suprafata in unitatea de timp:
forta · deplasare
pef2 pef2
I = ————————— = p·v = — = ——
(30)
suprafata
· timp
Zo r ·c
Ultima relatie este valabila pentru orice tip de unda.
– Nivelul presiunii sonore (sound pressure level, SPL) = logaritmul zecimal al raportului dintre presiunea acustica masurata si presiunea acustica de referinta po=2·10–5 Pa (presiune minima audibila la 1kHz):
Lp = log10(p/po) [in B, Bell-i] = 20·log10(p/po) [in dB] (31)
– Nivelul intensitatii sonore = logaritmul zecimal al raportului dintre intensitatea acustica masurata si intensitatea acustica de referinta, intensitatea minima audibila la 1000 Hz, Io=10–12 W/m2:
LI = log10(I/Io) [in B, Bell-i] = 10·log10(I/Io) [in dB] (32)
Nivelul unui sunet dat este acelasi in decibeli (dB) indiferent de faptul ca este exprimat ca nivel de presiune sau ca nivel de intensitate sonora.
Exemple
La cresterea cu 20 dB a nivelului intensitatii, intensitatea acustica a crescut de 100 de ori:
D L = L2 –L1 = 10·log(I2 /I1) = 10·log100=20 dB
I2 = I1·10 dL(dB) /10 (33)
iar presiunea sonora de 10 ori:
D L = L2 –L1 = 20·log(p2 /p1) = 20·log10=20 dB
p2 = p1·10 dL(dB) / 20 (34)
– Nivelul acustic (loudness level) este dat in decibeli acustici dB(A) (=Foni) si reprezinta curbe de egala senzatie auditiva.
Nivelul intensitatii (dB) functie de frecventa si nivelul
acustic (dBA)
| Nivel sonor dB(A)
Frecventa (Hz)? |
0
dBA |
20
dBA |
40
dBA |
60
dBA |
80
dBA |
100
dBA |
120
dBA |
|
20
|
70
|
80
|
90
|
101
|
112
|
128
|
145
|
|
100
|
25
|
37
|
51
|
68
|
85
|
103
|
125
|
|
200
|
13
|
27
|
42
|
60
|
78
|
98
|
122
|
|
500
|
8
|
20
|
38
|
56
|
75
|
96
|
119
|
|
1000
|
5
|
20
|
40
|
60
|
80
|
100
|
120
|
|
3500
|
-3
|
13
|
33
|
50
|
70
|
88
|
105
|
|
8500
|
17
|
30
|
48
|
67
|
87
|
107
|
130
|
|
12000
|
11
|
23
|
40
|
57
|
78
|
104
|
140
|
|
15000
|
20
|
30
|
45
|
60
|
80
|
110
|
145
|
Figura
2. Curbele de nivel acustic functie de frecventa.
Conservarea energiei ne asigura ca puterea "P" a sursei punctiforme ce emite izotrop (la fel pe toate directiile spatiului) se leaga de intensitatea sonora "I" la distanta "r" de sursa prin relatia:
P = I·4·p ·r 2 I=P/(4·p ·r 2) [I]SI = W/m2 (35)
Intensitatea undei sferice se leaga de presiunea sonora "p" prin relatia:
I= p2/(r ·c) (36)
de unde presiunea sonora efectiva este:
p = [P·r ·c/(4·p )]1/2 / r (37)
Daca sursa emite doar intr-o jumatate a spatiului (oscileaza intr-un perete) unghiul solid sub care emite este doar 2p si relatia devine:
P = I·2·p ·r 2 I=P/(2·p ·r 2) (38)
Cand sursa oscileaza pe muchia dintre doi pereti unghiul solid sub care emite este p si :
I=P/(p ·r 2) (39)
Cand sursa este plasata intr-un colt al camerei unghiul solid sub care emite este p /2 si :
I=2·P/(p ·r 2) (40)
– Densitatea energiei sonore (E) = energia undei din unitatea de volum
E = I/c [J/m3] pentru unda plana (41)
Pentru o unda plana avem relatiile:
I= p2/(r ·c) si v =p/(r ·c) deci I= v2·r ·c = w2·x2·r ·c (42)
Aici produsul "r ·c" este impedanta acustica specifica a mediului care pentru aer la 20oC si 760 mm Hg are valoarea:
r ·c = 1,21 kg/m3 · 344m/s = 416 kg/(s·m2)