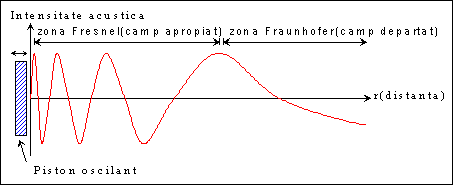
 Figura
1. Campul acustic cu delimitarea dintre campul apropiat (zona Fresnel)
si campul departat (zona Fraunhofer).
Figura
1. Campul acustic cu delimitarea dintre campul apropiat (zona Fresnel)
si campul departat (zona Fraunhofer).
Actiunea pistonului asupra mediului
Avem un piston circular de raza "a" care oscileaza armonic intr-un orificiu de raza "a" dintr-un panou cu dimensiuni foarte mari (panou infinit care divide spatiul in doua semispatii). Se separa astfel undele radiate de cele doua fete ale pistonului. Zona din spatiu in care se emit undele acustice se numeste camp acustic . In cadrul campului acustic deosebim campul apropiat (zona Fresnel) pentru distante r< a2/l si campul indepartat (zona Fraunhofer) pentru distante r>a2/l . In zona Fresnel presiunea acustica si intensitatea au maxime si minime, anulandu-se in anumite puncte din spatiu. In zona Fraunhofer presiunea acustica si intensitatea au o comportare lina cu distanta, scad ca "1/r" si respectiv "1/r2".
 Figura
1. Campul acustic cu delimitarea dintre campul apropiat (zona Fresnel)
si campul departat (zona Fraunhofer).
Figura
1. Campul acustic cu delimitarea dintre campul apropiat (zona Fresnel)
si campul departat (zona Fraunhofer).
Pentru campul apropiat variatia cu pozitia a intensitatii acustice este data de expresia:
I = Io·sin2[(p /l )·(a2+r2)1/2 – r] (1)
unde Io este valoarea maxima a intensitatii acustice. Cazurile de interes sunt:
–minime I=0 la r = (a2 – n2·l2)/(2·n·l ) (2)
–maxime I=Io la r = [a2 – (2·n+1)2·l2/4] / [(2·n+1)·l ) (3)
unde "n" este un numar intreg. Ultimul maxim al intensitatii apare la n=0, cand:
r lim = a2/l –l /4 » a2/l (4)
si delimiteaza zona Fresnel de zona Fraunhofer.
Pentru campul indepartat expresia presiunii acustice produse de piston intr-un punct P aflat la distanta "r" de centrul pistonului pe o dreapta ce face unghiul "q " cu axa de simetrie a pistonului este:
p(r) = j·Zo·vo·e j(w ·t–k·r)·[2·J1(k·a·sinq ) / (k·a·sinq )]·k·a2/(2·r) (5)
unde:
J1(x)@ (x/2)·(1–x2/8)
pentru x ® 0
(6)
J1(x)@ [2/(p
x)]1/2 ·sin(x–p /4) pentru x ®
infinit (7)
Functia de directivitate definita ca:
presiunea la distanta "r" pe directia de unghi "q
"
D(q ) = ————————————————————
(8)
presiunea la distanta "r" pe axa de simetrie
are in cazul pistonului urmatoarea expresie:
D(k·a·sinq ) = 2·J1(k·a·sinq ) / (k·a·sinq ) (9)
Functia de directivitate are valoare maxima cand q ? 0:
D(q ) = [2·J1(k·a·sinq ) / (k·a·sinq )] =>1 (q=> 0) (10)
Concluzie => presiunea acustica este maxima pe axa de simetrie.
Functia de directivitate [2·J1(k·a·sinq ) / (k·a·sinq )] se anuleaza pentru anumite valori ale argumentului " k·a·sinq ":
k·a·sinq = 3,83 sau 7,02 sau 10,15 sau… (11)
Pentru prima valoare putem afla unghiul la care se anuleaza presiunea folosind relatia:
sinq = 3,83/(k·a) (12)
Cea mai mare valoare ce o poate lua sinq este 1 (q =p /2). De aici se poate deduce cea mai mare lungime de unda pentru care se anuleaza presiunea la q = p /2:
l1 = 2·p ·a/3,83 @ p ·a/2 (13)
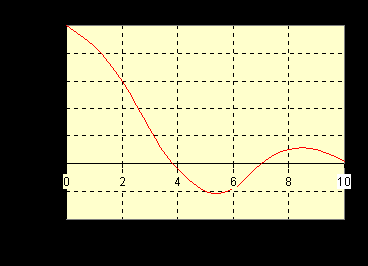
Figura 2. Graficul functiei de directivitate
a pistonului.
Pentru lungimi de unda mai mari decat l1 pistonul radiaza pe toate directiile, cu atat mai uniform cu cat lungimea de unda e mai mare. Pentru lungimi de unda mai mici decat l1 pistonul radiaza directiv, cu atat mai directiv cu cat e mai mica lungimea de unda. Unghiul la care se anuleaza presiunea devine din ce in ce mai mic, cu cat scade lungimea de unda:
sinq1 @ 2·l /(p ·a) (14)
fasciculul radiat devenind din ce in ce mai ingust. Marind frecventa de oscilatie a pistonului, implicit micsorand lungimea de unda a semnalului acustic emis, se formeaza si alte maxime de emisie, lobi de radiatie secundari delimitati de unghiurile q1, q2, q3, etc. Intensitatile acustice in lobii secundari sunt mult mai mici decat intensitatea lobului principal central. Astfel in primul lob secundar (cuprins intre unghiurile q1 si q2) se emite mai putin de 2% din intensitatea lobului principal.
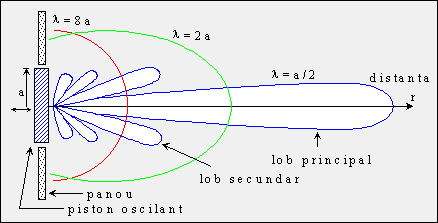
Figura 3. Pistonul emite diferit pentru
lungimi de unda diferite.