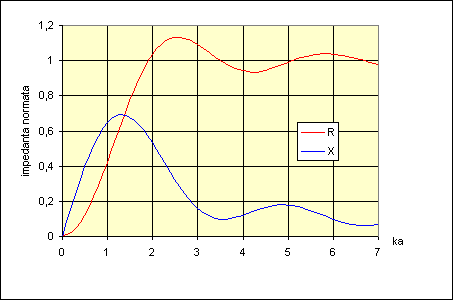
Figura 4. Graficul rezistentei R si reactantei X mecanice normate a unui piston oscilant.
Pistonul care oscileaza simte o forta de reactie din partea mediului in care oscileaza. Raportul dintre forta cu care trebuie actionat pistonul (egala in modul cu forta de reactie a mediului) si viteza de oscilatie a pistonului reprezinta impedanta mecanica de radiatie:
Zr = F/v (15)
si are expresia:
Zr = ro·co·p ·a2·[1–2·J1(2ka)/(2ka) + j·2·K1(2ka)/(2ka)2] (16)
unde:
J1(x)@ [2/(p x)]1/2 ·sin(x–p /4); K1(x)@ 2x/p pentru x ® infinit (19)
Deducerea expresiei se face insumand pe intreaga suprafata a pistonului influenta presiunii create de un element dS al suprafetei pistonului asupra altui element de suprafata dS? tot al pistonului.
Rezistenta de radiatie este partea reala a impedantei si are expresia:
rr = ro·co·p ·a2·[1–2·J1(2ka)/(2ka)] (20)
Rezistenta de radiatie este generata de componenta fortei care este in faza cu viteza de oscilatie. Ea arata transferul real de putere dintre sistemul mecanic al pistonului si sistemul acustic al mediului elastic.
Reactanta de radiatie, partea imaginara a impedantei, are expresia:
xr = ro·co·p ·a2·2·K1(2ka)/(2ka)2 (21)
Reactanta de radiatie e generata de componenta fortei in cuadratura cu viteza de oscilatie (defazata cu 90o). Ea este legata de schimbul reactiv de putere, putere ce este transferata mediului care la un moment ulterior o returneaza sistemului mecanic oscilant.
Impartind ambele expresii cu "ro·co·p ·a2" obtinem valorile normate ale rezistentei de radiatie "R" si reactantei de radiatie "X":
R(2ka) = rr / (ro·co·p ·a2) = [1–2·J1(2ka)/(2ka)] (22)
X(2ka) = xr / (ro·co·p ·a2) = 2·K1(2ka)/(2ka)2 (23)
unde:
Functiile R si X sunt reprezentate grafic in figura
4 in functie de marimea k·a = 2·p ·a/l
= 2·p ·n ·a/c.

Figura 4. Graficul rezistentei R si reactantei
X mecanice normate a unui piston oscilant.
Pentru un piston dat (raza "a" este fixa) se vede ca rezistenta de radiatie creste cu frecventa pana la o valoare maxima, de unde ramane aproximativ constanta. Reactanta de radiatie creste si ea la inceput cu frecventa, apoi scade destul de repede.
La frecvente joase, cand k·a<1, expresiile rezistentei de radiatie si reactantei de radiatie in valori normate le putem scrie ca:
R(2·k·a) @ (k·a )2/2 = (w ·a)2/(2·c2) (26)
X(2·k·a ) @ 8·k·a /(3p ) = 8·w ·a/(3·p ·c) (27)
Stiind ca reactanta mecanica a unei mase este "w ·m" putem defini masa de radiatie prin relatia:
mR = xR /w = p ·a2·r0·X1(2ka)/k (28)
Masa de radiatie reprezinta masa de aer antrenata in miscare oscilatorie de catre pistonul vibrant. Pentru frecvente joase, conform relatiei, este:
mr = r ·c·p ·a2·8·w ·a/(3·p ·w ·c) = 8·r ·a3 /3 (29)
La frecvente inalte, ka>3, expresiile rezistentei de radiatie si reactantei de radiatie in valori normate sunt:
R(2·k·a) @ 1 (30)
X(2·k·a) @ 2/(p ·k·a) = 2·c/(p ·w ·a) » 0 (31)