 Figura
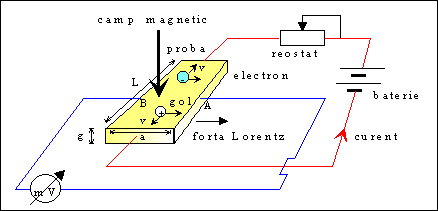
1. Montaj experimental pentru masurarea efectului Hall.
Figura
1. Montaj experimental pentru masurarea efectului Hall.
Studiem in aceasta lucrare unul dintre cele mai importante efecte galvano-magnetice, efect care permite determinarea foarte precisa a concentratiei precum si a tipului de purtatori care participa la conductie.
Consideratii generale
Vom considera un semiconductor omogen, de forma paralelipipedica, prin care trece un curent electric, asa cum este aratat in figura1. Diferenta de potential intre punctele A si B, situate in acelasi plan perpendicular pe liniile de curent (suprafata echipotentiala), este nula in absenta campului magnetic constant, H. Daca exista un camp magnetic, perpendicular pe directia curentului, intre punctele A si B apare o diferenta de potential; acest fenomen se numeste efect Hall, iar diferenta de potential care exista intre punctele Asi B, tensiune Hall.
 Figura
1. Montaj experimental pentru masurarea efectului Hall.
Figura
1. Montaj experimental pentru masurarea efectului Hall.
Pentru a vedea mecanismul de aparitie si modul in care depinde aceasta tensiune de intensitatea curentului care trece prin proba, marimea campului magnetic si dimensiunile probei, vom considera miscarea unei sarcini electrice e, cu viteza v, in campul magnetic B. Asupra acestei sarcini va actiona forta Lorentz:
F = e v ´ B , "e" isi contine semnul (1)
Prin actiunea ei sarcinile, indiferent de semnul lor, vor fi deviate catre aceeeasi suprafata. Singura conditie care se cere indeplinita este ca sensul de miscare al sarcinilor sa fie compatibil cu sensul curentului ce trece prin proba. Deplasarea sarcinilor spre o suprafata modifica incarcarea electrica a acesteia conducand la aparitia unei diferente de incarcare electrica intre suprafetele SA si SB.
In interiorul probei ia nastere un camp electric EH care genereaza o forta contrara fortei Lorentz. Astfel dupa o incarcare electrica suficienta a suprafetelor SA si SB, restul purtatorilor trec nedeviati prin proba. Scriind aceasta egalitate dintre forta generata de incarcarea electrica a suprafetelor si forta Lorentz:
e E H = e v ´ B (2)
si cunoscand legatura care exista intre densitatea de curent, viteza purtatorilor si concentratie:
j = e n v
obtinem:
n EH = j ´ B /e (3)
Luand in considerare dimensiunile probei asa cum sunt indicate in figura 1, pentru tensiunea Hall se obtine:
UH = RH × I× B/g , unde RH =1/ne (4)
Din aceasta expresie se vede ca semnul diferentei de potential depinde de semnul purtatorilor liberi, pentru conductie de electroni RH <0, iar pentru conductie de goluri RH >0. Cunoscand constanta Hall RH se poate determina concentratia purtatorilor de curent.
Totusi in obtinerea relatiei (4) consideratiile simple pe care le-am folosit nu au permis luarea in considerare a caracterului statistic al vitezelor purtatorilor de curent precum si a mecanismelor de imprastiere. In cele ce urmeaza, vom schita, numai, obtinerea coeficientului Hall, cu ajutorul ecuatiei cinetice Boltzman, indicand pentru completare, lucrarea [1]. Ecuatia cinetica Boltzman permite determinarea, in anumite conditii, a corectiei la functia de distributie de echilibru, fenomenele de neechilibru termodinamic putand fi descrise de acest termen corectiv. Pentru un semiconductor cu suprafete energetice sferice si in cazul ciocnirilor elestice, ecuatia de transport are o forma relativ simpla, permitand gasirea cu usurinta a corectiei la functia de distributie. Cu acest termen, pentru fenomenele galvano-magnetice: E ^ H, ? T=0, ? F=0, obtinem ecuatiile pentru componentele curent:
Deoarece campurile magnetice la care lucram sunt astfel incat verifica ingalitatea ??H <<1, aceasta fiind conditia de camp mic pentru efectul Hall, dezvoltand in serie si pastrind termenii adecvati, obtinem:
RH = (1/nec)×<t2>/<t>2 (8)
Remarcam aparitia factorului corectiv f=<t2>/<t>2, spre deosebire de expresia obtinuta prin consideratii simple; cum intotdeauna exista ingalitatea <t2> > <t>2, acest factor corectiv este mai mare ca 1. Uzand de diferite dependente de energie pentru timpul de relaxare [1], putem gasi, functie de mecanismul de imprastiere care predomina, factorul corectiv. Astfel, la temperaturi inalte, f=3p /8 iar pentru cele joase f=1,93.
Cunoscand, pentru una si aceeasi proba, constanta Hall RH si conductibilitatea s , in cazul in care exista un singur tip de purtatori care participa la conductie, se poate gasi mobilitatea purtatorilor de curent:
mH =s R (9)
Pentru semiconductorii cu conductie de ambele feluri, lucrurile sunt mai complicate, expresiile pentru coeficientul Hall si conductibilitate fiind:
s =nemn+ pemp
R=(1/e) [(pm2p– nm2n)/(pmp+ nmn)2]× [<t2>/<t>2] (10)
Montajul experimental
Montajul experimetal, asa cum este prezent schematic in figura 1, consta din doua mari circuite :
– circuitul de alimentare al probei cu un curent I,
– circuitul pentru masurarea diferentei de potential Hall.
Curentii de lucru, care trec prin proba sunt de ordinul zecilor de mA. Ca metodica de masurare se traseaza curbele UH=U(H)I=const. si UH=U(I)H=const. obtinandu-se din prelucrarea lor, concentratia. Masurand conductibilitatea probei se poate gasi mobilitatea Hall.
Efecte parazite
In afara de cazul banal al unei tensiuni suplimentare care poate sa apara datorita plasarii incorecte a contactelor A si B (adica nu apartin aceleasi suprafete echipotentiale) mai apar si alte efecte.
Efectul Ettinghausen consta in aparitia unui gradient de temperatura dupa directia y, in prezenta campului magnetic. Gradientul conduce la aparitia unei forte motoare care are acelasi sens cu tensiune Hall si deci este foarte greu de separat de acesta. Legatura dintre gradientul de temperatura si marimile jx si Hz este data in (11), unde P este un coeficient:
P = (¶ T/¶ y)/ (jHz ) (11)
Daca exista un gradient de temperatura dupa directia x, dupa directia y apare, in prezenta campului magnetic, o forta electromotoare Ey dupa legea:
Ey=Q^ (¶ T/¶ x) Hz (12)
Unde Q^ este coeficientul Nernst- Ettinghausen transversal, efectul acesta purtand numele de efect N-E transversal.
Efectul Righi-Leduc consta in faptul ca daca exista un gradient de temperatura dupa directia x, atunci, sub actiunea campului magnetic, apare un gradient de temperatura dupa y, acesta conducand la aparitia unei forte termoelectromotoare care altereaza efectul Hall. Coeficientul Righi-Leduc este:
S= ¶ T/¶ y /( Hz ¶ T/¶ x) (13)
Astfel, tensiunea masurata cu potentiometrul compensator, V1 eate de fapt o suma la care isi aduc cotributia efectele anuntate anterior:
V1=VH+VE+VNE+VRL+VI (14)
unde VI apare ca urmare a plasarii incorecte a contactelor. Prin inversari adecvate ale curentului ce trece prin proba, precum si a campului magnetic, dupa metodica data mai jos, se obtine:
V2= VH –VE +VNE +VRL–VI (I inversat)
V3= VH +VE –VNE –VRL–VI (I si H inversat) (15)
V4= –VH –VE –VNE –VRL+VI (H inversat)
Obtinem deci pentru suma dintre tensiunea Hall si cea Ettinghausen:
VH +VE = (V1 –V2 +V3 –V4)/4 (16)
Bibliografie
1. P. S. Kireev - "Fizica semiconductorilor", Editura Stiintifica si Enciclopedica 1977.