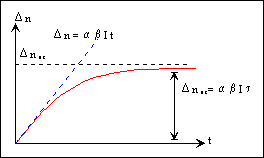
Figura 1. Evolutia in timp a concentratiei purtatorilor de neechlibru generati prin iluminare.
1. Introducere
Purtatorii liberi apar intr-un semiconductor datorita excitarii electronilor din banda de valenta sau de pe nivelele donoare in banda de conductie sau pe nivelele acceptoare. Energia necesara excitarii este asigurata in mod normal de energia termica a retelei, astfel ca temperatura electronilor si a retelei este aceeasi. Acestia sunt purtatorii de sarcina de echilibru. Daca semiconductorul este iluminat apar purtatori de sarcina suplimentari cu energie mai mare in momentul aparitiei decat a purtatorilor de echilibru si din aceasta cauza sunt numiti purtatori de neechilibru sau purtatori in exces. Purtatorii de neechilibru interactionand cu reteaua cristalului isi reduc energia la valoarea energiei purtatorilor de echilibru intr-un interval de timp foarte scurt, 10-12¸10-10s, comparativ cu timpul de viata al purtatorilor in semiconductori.
Conductivitatea electrica de neechilibru
Iluminand un semiconductor, concentratia purtatorilor liberi devine :
n = no + D n, p = po + D p (1)
unde no si po sunt concentratiille de echilibru ale electronilor si golurilor, iar D n si D p sunt concentratiile electronilor si golurilor de neechilibru aparute ca urmare a injectiei optice. Conductivitatea electrica se va putea exprima si ea ca :
s = so + Ds (2)
in care conductivitatea de neechilibru este:
Ds = q · (mn·D n + mp·D p) (3)
unde:
D n = D p = a·b·I·t (4)
reprezentata punctat in figura 1, unde:
D n' = a·b·I·tn , D p' = a·b·I·tp (5)
unde tn si tp reprezinta timpul mediu de viata al electronilor, respectiv golurilor.

Figura 1. Evolutia in timp a concentratiei
purtatorilor de neechlibru generati prin iluminare.
Putem rescrie conductivitatea de neechilibru ca:
Ds = q·a·b·I·(tn·mn + tp·mp ) (3')
Cand unul din termeni este mult mai mare decat celalalt avem relatia:
Ds = q·a·b·I·t ·m (3")
in care conductivitatea de neechilibru este determinata de patru parametri :
– a si b => caracterizeaza interactiunea luminii cu semiconductorul;
– t si m => interactiunea purtatorilor de sarcina cu semiconductorul.
Timpul de viata al purtatorilor de neechilibru
Probabilitatea ca un electron sa intalneasca un gol este proportionala cu concentratia golurilor p si cu viteza relativa medie de deplasare a electronului in raport cu golul vn . Timpul de viata al electronilor tn depinde invers proportional de concentratia de goluri si de coeficientul de captura Cn = vn·Sn (Sn fiind sectiunea de captura) :
tn = 1/(p·Cn) (6)
Relaxarea fotoconductiei
Daca la momentul t=0 incepe iluminarea semiconductorului, conductivitatea electrica stationara se atinge dupa un anumit timp, iar la incetarea iluminarii ea scade treptat la valoarea de echilibru. Curbele de crestere sau descrestere a conductiei de neechilibru pentru diferite intensitati ale radiatiei incidente se numesc curbe de relaxare a conductiei de neechilibru.
Recombinarea electronilor de neechilibru cu golurile este liniara in cazul in care exista un singur tip de goluri cu concentratie mare si practic independenta de intensitatea radiatiei, rata recombinarii fiind atunci:
R = D n/tn = D n × p × Cn (7)
Variatia concentratiei purtatorilor de neechilibru in unitatea de timp se poate scrie:
dD n/dt = abI - D n/t (8)
cu solutia:
D n = abIt (1- e - t/t) (9)
daca la t = 0 proba se ilumineaza.
Daca la t = 0 inceteaza iluminarea atunci variatia concentratiei purtatorilor de neechilibru in unitatea de timp se poate scrie:
dD n/dt = - D n/t (10)
cu solutia :
D n = abIt e - t/t(11)
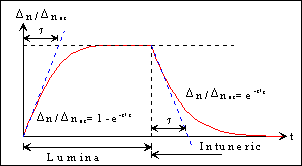
Figura 2. Curbe ale evolutiei in timp a
concentratiei purtatorilor de neechilibru la iluminare si la intuneric.
Daca concentratiile de echilibru sunt mici, iar purtatorii de neechilibru se obtin prin excitarea electronilor din banda de valenta in banda de conductie, avem egalitate intre concentratiile de neechilibru ale electronilor si golurilor si din relatia (7) avem recombinare patratica:
R = D n · p · C = C·D n ·D p = C·(D n)2 (7')
Pentru iluminare ecuatia evolutiei in timp a concentratiei de neechilibru este:
dD n/dt = abI - C× (D n)2 (8')
cu solutia:
D n = (a·b·I/C)1/2 · th [t · (a·b·I)1/2] (9')
Pentru conditia de intuneric avem relatia:
dD n/dt = - C× (D n)2 (10')
cu solutia:
D n = (a·b·I/C)1/2 / [t · (abI)1/2 +1] (11')
In acest caz al recombinarii patratice nu se poate introduce notiunea de timp de viata al purtatorilor de neechilibru t =1/(CD p), fiindca el depinde prin D p de intensitatea radiatiei incidente. Se poate defini pentru purtatorii de neechilibru doar un timp de viata instantaneu.
Metode pentru masurarea fotoconductiei
In cazul in care D n >> no , masurarea fotoconductiei se face simplu prin masurarea curentului care trece prin circuitul fotorezistentei alimentate de la o sursa de tensiune constanta. Surplusul de curent la iluminare se masoara pe fondul curentului de intuneric. Daca D n << no , relatie ce are loc pentru semiconductorii cu rezistivitate mica, se folosesc montaje care elimina printr-un procedeu specific curentul de intuneric (montaj in punte sau compensator).
Daca la intuneric proba are reristenta R0, iar dupa iluminare rezistenta scade cu D R, tinand cont de expresia rezistentei in functie de geometria probei :
R0- D R = L / [S·(so + Ds )] (12)
putem calcula conductivitatea de neechilibru Ds ca:
Ds = (S/L) D R/[R0 (R0- D R)] (13a)
Ds /so = D R/(R0 - D R) (13b)
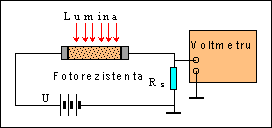
Figura 3. Masurarea raspunsului stationar
al unei fotorezistente.
Daca fotorezistenta se afla in serie cu o rezistenta de sarcina R s si o sursa de tensiune U, atunci modificarea tensiunii pe rezistenta de sarcina datorita iluminarii este:
D U s = (IL - Io) R s (14)
unde:
Io = U/(R s + Ro)
IL = U/(R s + Ro - D R)
si in consecinta avem:
D R = D Us (R s + Ro)2 / [U R s + D Us (R s + Ro)] (15)
Daca rezistenta de sarcina este mult mai mica decat fotorezistenta R s << Ro - D R atunci relatia (15) devine:
D R = D Us Ro2 / (U R s + D Us Ro) (16)
iar relatia corespunzatoare pentru conductivitatea de neechilibru (13a) este:
Ds = (S/L)·D Us / (U·R s) (17)
Regimul de masurare descris se numeste "regim de camp constant".
Procedura experimentala
1. Se realizeaza montajul din figura si se masoara Ds in regim de camp constant. Calculele se fac cu relatia (17).
2. Se verifica proportionalitatea dintre intensitatea radiatiei incidente si Ds modificand distanta dintre sursa de lumina si proba. Graficul Ds = f (1/d2), unde "d" este distanta sursa-proba, trebuie sa fie liniar fiindca iluminarea unei suprafete de catre o sursa punctiforma scade cu inversul patratului distantei dintre sursa si suprafata.
3. Pentru a evalua timpul de viata al purtatorilor in exces se va ilumina proba cu un fascicul de lumina intrerupt periodic (chopperat) si semnalul cules de pe rezistenta de sarcina se aplica unui osciloscop.
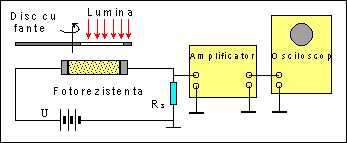
Figura 4. Masurarea raspunsului dinamic
al unei fotorezistente.
Bibliografie
1. Constantinescu, C., Glodeanu, A. - "Stari locale in semiconductori", Editura tehnica 1967, pag. 271-299, 379-387.
Morant => purtatorii minoritari in exces controleaza comportarea
ambelor tipuri de purtatori (modificarea densitatii purtatorilor majoritari
e mica procentual, ei apar ca reactie la prezenta minoritarilor)