1. Consideratii generale

Este cunoscut faptul ca daca un semiconductor este iluminat apare o forta fotoelectromotoare numai in urmatoarele doua cazuri:

1. daca semiconductorul este iluminat neuniform
2. daca in semiconductorul iluminat exista un camp electric, magnetic, gradient de impuritati sau un gradient de temperatura.

Ne vom ocupa numai de comportarea unui semiconductor iluminat in care exista un camp electric intern cauzat de prezenta gradientilor impuritatilor donoare si acceptoare. Daca este iluminata regiunea n a jonctiunii p-n atunci in vecinatatea suprafetei se vor crea perechi electron-gol a caror concentratie va scadea treptat spre interiorul semiconductorului. Sa presupunem ca stratul de baraj al jonctiunii se afla la o distanta comparabila cu lungimea de difuzie a putatorilor. In acest caz perechea elecron-gol intand in campul intern al stratului de baraj va fi separata. Electronii vor fi dirijati spre regiunea n a jonctiunii iar golurile spre regiunea p. Prin urmare echilibrul termodinamic al jonctiunii este perturbat, iar acest lucru se materializeaza prin aparitia unei diferente de potential care cauzeaza trecerea unui curent prin circuitul exterior al fotoelementului.

2. Teoria efectului fotoelectric in jonctiunea p-n

Teoria efectului fotoelectric in jonctiunea p-n a fost facuta de Cummerow care pentru a calcula caracteristica curent-tensiune in functie de radiatia incidenta a facut urmatoarele ipoteze:

• grosimea stratului de baraj "2d " este mica in comparatie cu l_p si l_n (grosimile regiunilor p si respectiv n), cat si in comparatie cu lungimile de difuzie ale electronilor L_n si golurilor L_p;
• campul electric in afara stratului de baraj este mic asa ca poate fi neglijat;
• concentratiile golurilor in regiunea p si ale electronilor in regiunea n sunt mici, asa ca peste tot se poate folosi statistica Boltzmann (nedegenerare).

Conform ipotezelor facute I_p(0)=I_p(d) si I_n(0)=I_n(d) si deci putem scrie:

A doua ipoteza conduce la relatiile:

unde D_n si D_p sunt coeficientii de difuzie a electronilor si respectiv golurilor iar q este sarcina electronului. Prin urmare, pentru a calcula curentii trebuie sa cunoastem distributia purtatorilor de neechilibru pe lungimile regiunilor n si p.

Folosind ecuatia de conservare a numarului de goluri, putem scrie urmatoarea ecuatie diferentiala pentru concentratia golurilor din regiunea n, in regim stationar:

unde p_n este concentratia de echilibru a golurilor din regiunea n, g (x) este numarul de goluri creat de lumina in unitatea de timp si volum iar t_p este timpul de viata al golurilor. Aceasta ecuatie se rezolva folosind urmatoarele conditii la limita:

Daca pe unitatea de suprafata a regiunii p la x = –l_p cad in unitatea de timp H_s cuante si fiecare cuanta creaza un electron atunci putem scrie:

unde (l/L_l) este coeficientul de absorbtie a luminii. Prin urmare, ecuatia diferentiala (4) se poate transcrie astfel:

Solutia acestei ecuatii cu conditia la limita (5) este,

unde

O expresie analoaga se poate gasi si pentru concentratia electronilor in regiunea p. Folosind aceste ecuatii si relatiile (2) si (3) pentru curentul total care trece prin jonctiune obtinem urmatoarea expresie:

unde: g_n = n_p /j_n si g_p = n_n /j_p reprezinta vitezele de generare termica a purtatorilor iar L_p este lungimea de difuzie efectiva a golurilor in regiunea n a jonctiunii si este data de expresia:

In cazul cand l_n >>L_p se poate scrie ca L_p' @ L_p g_o este viteza de generare optica a perechilor electron-gol in punctul x=0 si este data de formula:

L_l este adancimea efectiva unde are loc generarea de perechi electon-gol sub actiunea luminii in regiunea n a jonctiunii p-n si este data de:

O expresie analoaga se poate scrie si pentru L₂. Introducand notatiile:

obtinem formula finala pentru caracteristica curent-tensiune a fotoelementului:

Primul termen din (11) coincide cu caracteristica curent-tensiune a unei jonctiuni p-n la intuneric. Al doilea termen din (11) este proportional cu intensitatea radiatiei incidente si reprezinta fotocurentul.

Trebuie subliniat faptul ca efectele de suprafata pot influenta considerabil functionarea fotoelementelor. Pentru a lua in considerare in calculele facute mai sus efectele de suprafata ar trebui modificata conditia la limita (5) astfel:

unde s este viteza de recombinare la suprafata. Aceasta conditie la limita inseamna ca are loc un proces suplimentar de recombinare datorita difuziei purtatorilor spre suprafata. O conditie analoaga trebuie folosita si pentru x=l_p. In final se obtine o formula de tipul (7) unde marimile L_p,L_n,L₁ si L₂ vor contine si vitezele de recombinare pe cele doua suprafete ale fotoelementului.

3. Schema echivalenta a fotoelementelor

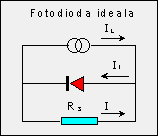
Folosind rezultatele teoretice de mai sus, putem asocia unui fotoelement o schema echivalenta care sa dea aceeasi caracterisctica curent-tensiune. Schema echivalenta simpla care descrie functionarea unui fotoelement la iluminarea continua este prezentata in figura 1.

Figura 1. Schema echivalenta a fotodiodei.

Actiunea luminii asupra fotoelementului este luata in coniderare in aceasta schema prin introducerea sursei de curent I_L a carei marime este determinata de intensitatea si compozitia spectrala a radiatiei incidente. Marimea I_L este egala cu curentul efectiv de electroni si goluri create de lumina si care nu au reusit sa recombine pana la procesul de separare din stratul de baraj. Recombinarea perechilor de electroni si goluri create de lumina este reprezentata in schema prin introducerea barierei inactive fotoelectric prin care trece curentul I₁. In circuitul exterior prin rezistenta de sarcina R_s trece curentul I. Din aceasta schema se poate observa ca:

Daca U este tensiunea pe rezistenta de sarcina si implicit pe stratul de baraj atunci:

In cazul unei jonctiuni p-n abrupte pentru I_s se obtine expresia:

unde s_i este conductibilitatea semiconductorului intrisec, b este raportul mobilitatilor, r sunt rezistivitatile regiunilor n si respectiv p ale jonctiunii, L_n si L_p sunt lungimile de difuizie ale electronilor si respectiv golurilor iar S este suprafata jonctiunii.

Din (13) si (14) se poate obtine formula:

care reprezinta familia de caracteristici curent-tensiune a fotoelementului, parametru fiind intensitatea radiatiei incidente.

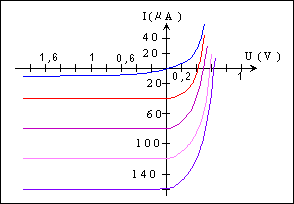
Figura 2. Caracteristica curent tensiune a fotodiodei la diverse iluminari.

In figura 2 este prezentata o familie de caractereistici curent-tensiune, a unui fotoelement din Si pentru diferite intensitati ale radiatiei incidente. Curba care trece prin originea axelor de coordonate corespunde lui I_L = 0 (lipsa iluminarii). Din figura 2 putem observa ca, odata cu cresterea intensitatii radiatiei incidente, caracteristicile curent-tensiune se deplaseaza in jos si ca in cadranul IV al sistemului de axe apar portiuni de caracteristici curent-tensiune. Pe aceste portiuni, jonctiunea p-n iluminata se comporta ca o sursa de curent iar circuitul exterior ca o rezistenta de sarcina. Diferite puncte ale caracteristicilor situate in cadranul IV corespund diferitelor rezistente de sarcina. Punctul unde caracteristica taie axa tensiunilor corespunde rezistentei de sarcina R_S = ? , iar cel unde taie axa curentilor lui R_S =0.

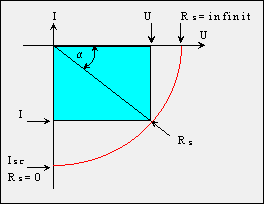
Figura 3. Elementele importante ale caracteristicii I-V din cadranul 4.

In figura 3 este aratata portiunea de caracteristica curent-tensiune discutata mai sus si care nu reprezinta altceva decat portiunea de sarcina a fotoelementului in care functioneaza ca transformator al energiei luminoase in energie electrica. Daca fotoelementul este scurtcircuitat (R_s=0) atunci in circuit se stabileste curentul I_sc a carui marime este determinata de calitatea fotoelementului si intensitatea radiatiei incidente.

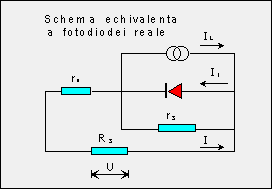
Figura 4. Schema echivalenta reala (completa) a fotodiodei.

Analiza facuta mai sus, rezulta din schema echivalenta simpla a fotoelementului din figura 1 care nu tine seama de existenta rezistentei serie a jonctiunii p-n, de rezistenta contactelor sau de rezistenta de scurgere. In figura 4 este prezentata schema echivalenta reala a unui fotoelement iar r_d este rezistenta serie a jonctiunii p-n. In acest caz caracteristica curent-tensiune a fotoelementului are urmatoarea forma:

care se poate deduce usor din schema echivalenta (fig. 4).

Pentru fotoelemente se mai defineste sensibilitatea integrala care este raportul dintre diferenta curentilor la lumina si intuneric exprimata in mA si valoarea fluxului de lumina cu compozitia spectrala corespunzatoare radiatiei wolframului incalzit la 2840 K, exprimat in lumeni. Aceasta definitie presupune implicit ca sensibilitatea fotoelementului nu depinde de intensitatea fluxului luminos sau ca fotocurentul variaza liniar cu fluxul incident. Acest fapt este valabil numai in cazul iluminarilor slabe cand rezistenta stratului de baraj ramanne mai mare decat rezistenta serie a fotodiodei. O alta cauza a neliniaritatii fotocurentului in functie de intensitatea luminii la intensitati mari consta in aceea ca timpul de viata al purtatorilor minoritari depinde de nivelul injectiei (in cazul de fata de intensitatea luminii).

4. Instalatia experimentala

In instalatia experimentala se masoara tensiunea fotoelectromotoare si caracteristicile curent-tensiune la intuneric si diferite intensitati ale radiatiei incidente. Tensiunea fotoelectromotoare se poate gasi din (16) facand I=0 si deci vom avea:

Daca se introduce o rezistenta de sarcina R_s in serie cu fotodioda atunci va trece un curent I = - U_f / R_S si deci din (16) obtinem:

Ecuatia (19) descrie functionarea fotoelementelor atunci cand ele functioneaza ca transformatoare de energie luminoasa in energie electrica.

Daca fotoelementul este polarizat invers cu tensiunea atunci (19) se modifica astfel:

Expresia (20) reprezinta ecuatia fundamentala a fotoelementului in regim de fotodioda. La tensiuni inverse mari I @ I_L + I_S , iar pentru tensiuni directe U>U_f obtinem ecuatia obisnuita a unei jonctiuni p-n.

Tensiunea fotoelectromotoare se masoara cu ajutorul unui voltmetru digital cu rezistenta de intrare mare, pentru diferite intensitati ale radiatiei incidente. Conectand fotodioda in serie cu o sursa de tensiune U reglabila si cu o rezistenta de sarcina R_s reglabila se poate ridica caracteristica curent-tensiune.

Daca tensiunea inversa aplicata fotodiodei este suficient de mare astfel incat curentul invers sa intre in regiunea de saturatie, atunci masurand tensiunea cu ajutorul voltmetrului pe o rezistenta cunoscuta putem determina marimea I_s+I_L cand fotoelementul este iluminat si I_s cand este la intuneric. Practic, pentru determinarea marimilor I_s si I_L, se ridica caracteristicile curent-tensiune la intuneric si la diferite intensitati ale radiatiei incidente, iar portiunile de saturatie ale curentilor se extrapoleaza la U=0.

Scopul lucrarii consta in verificarea principalelor caracteristici ale fotoelementelor folosind procedura descrisa mai jos.

1. Se masoara tensiunea fotoelectromotoare pentru diferite intensitati ale radiatiei incidente. Se construieste graficul U_f = f(1/d²) unde d este distanta de la sursa de lumina pana la fotodioda. Sa se explice rezultatul.
2. Fara sursa de tensiune in circuit se masoara tensiunea fotoelectromotare de pe rezistenta de sarcina R_s pentru diferite valori ale acesteia. Se face graficul U_f=f (R_s) pentru doua intensitati ale radiatiei incidente.
3. Se ridica caracteristicile curent-tensiune la intuneric si pentru diferite intensitati ale radiatiei incidente. Din rezultatele obtinute sa se gaseasca I_s si I_L si sa se verifice relatia (18). In acest scop pentru fiecare intensitate a luminii incidente trebuie masurata si tensiunea fotoelectromotoare.
4. Se ridica caracteristica lux-amper a fotoelementului masurand fotocurentul pentru diferite distante ale sursei de lumina pana la fotodioda. Se va trasa graficul I_L = f (F /d² ) unde F este fluxul luminos incident corespunzator sursei folosite si care se va da in laborator.
5. Se afle sensibilitatea integrala a fotoelementului studiat cu relatia:

Intrebari

1. Ce este rezistenta interna a jonctiunii p-n si cum se poate determina?

2. De ce sensibilitatea fotodiodei este mai mare la polarizare inversa decat la cea directa?