 Figura
1. Transformarile termodinamice suferite de gaz.
Figura
1. Transformarile termodinamice suferite de gaz.
Consideratii teoretice
Se numeste caldura molara cantitatea de caldura absorbita de un mol de substanta pentru a-si mari temperatura cu un grad. Dupa cum absorbtia de caldura la gaze are loc la volum constant sau la presiune constanta deosebim Cv si Cp:
Cv = dQv/dT (1)
Cp = dQp/dT (2)
Plecand de la principiul intai al termodinamicii :
dQ = dU + pdV = dH – Vdp (3)
Cp = dH/dT = d(U+pV)/dT = dU/dT+d(RT)/dT= Cv+R (5)
relatia lui Robert Mayer. In relatiile de mai sus U reprezinta energia interna, H entalpia, iar R constanta generala a gazelor perfecte.
Raportul Cp/Cv = g se numeste exponent adiabatic fiindca intevine in legea transformarii adiabatice. Se numeste adiabatica o transformare in timpul careia gazul nu schimba caldura cu mediul, iar una din formele legii ei este:
p·V? = const. (6)
Valoarea exponentului adiabatic depinde de numarul gradelor de libertate (i) ale gazului respectiv. In teoria cinetica a gazelor perfecte se arata ca:
g = (i+2)/i (7)
Exponentul g este o functie descrescatoare cu temperatura. In intervalul 0 - 2000°C, pentru gaze biatomice se poate folosi formula aproximativa:
g =1,4–0,5·10–4·t (8)
Cunoasterea exponentului adiabatic are importanta in studiul curgerii gazelor prin tuburi cu viteze sonice, atingerii vitezelor supersonice, calcului vitezei de propagare a sunetului prin gaze etc.
In lucrarea de fata se determina exponentul adiabatic folosind metoda Clement – Desormes. Se utilizeaza un vas de volum Vo ce comunica prin robinete cu exteriorul si cu o pompa. Presiunea din vas se masoara cu un manometru atasat.
 Figura
1. Transformarile termodinamice suferite de gaz.
Figura
1. Transformarile termodinamice suferite de gaz.
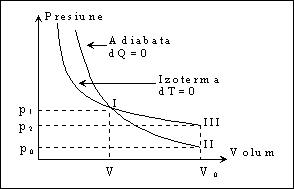
1. Se pompeaza gaz in balonul de volum Vo. Avem in vas masa "m" de gaz cu volum Vo si la stabilirea echilibrului termic cu exteriorul temperatura To si presiunea p1:
p1 = p0 + h1
unde p0 este presiunea atmosferica, h1 este diferenta de nivel intre nivelele lichidului din ramurile manometrului, iar presiunile se masoara in cm coloana lichid. Gazul ce ne intereseaza, cu masa mo<m, ar ocupa volumul V<Vo in aceleasi conditii de presiune si temperatura, p1 si To. Aceasta situatie corespunde starii I pe diagrama din figura 1.
2. Se destinde gazul adiabatic evacuand din balon gaz prin deschiderea urmata de reinchiderea rapida a robinetului de comunicare cu exteriorul, pana cand ajungem la presiunea atmosferica po. Acum avem in balonul cu volum Vo masa "mo" de gaz si temperatura TII mai mica decat To, corespuzator starii II din figura 1.
3. La stabilirea echilibrului termic cu mediul gazul preia caldura la volum vonstant Vo si ajunge la temperatura To a mediului si presiunea p2>po, corespuzator starii III din figura 1:
p2 = p0 + h2
unde h2 reprezinta noua diferenta de nivel a lichidului manometric.
Transformarea din starea I in starea II fiind adiabatica se poate scrie:
(p0+h1)·V? = p0·Vo? (9)
Starile I si III se afla pe o izoterma temperatura fiind To, deci:
(p0 + h1)·V = (p0 + h2)·Vo (10)
ridicand relatia (10) la puterea ? si impartind-o cu (9) se obtine :
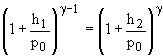 (11)
(11)Metoda experimentala
Dispozitivul experimental schitat in figura 2, se compune dintr-un balon B la care este atasat un manometru cu apa M. Balonul comunica prin robinetul R1 cu exteriorul, iar prin robinetul R2 cu pompa P.
Mod de lucru
1. Se inchide robinetul R1, se deschide R2 si se pompeaza aer in balonul B pana cand diferenta de nivel din manometru devine 10-20 cm.
2. Se inchide R2 si se asteapta stabilirea echilibrului termic cu mediul.
3. Se citeste valoarea diferentei de nivel din manometru h1 si se trece in tabel.
4. Se deschide rapid R1, pana cand presiunea gazului devine egala cu cea exterioara p0, apoi se inchide la loc. Se asteapta incalzirea gazului pana la temperatura mediului. La stabilirea echilibrului termic se citeste denivelarea h2 din manometru si se trece in tabel.
5. Se repeta operatiile de cel putin 5 ori.
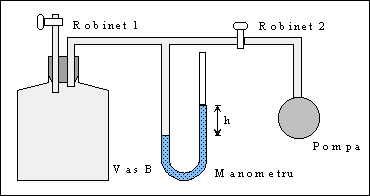 Figura
2. Dispozitivul experimental.
Figura
2. Dispozitivul experimental.
Prelucrarea datelor experimentale
Cu relatia (12) se calculeaza
exponentul adiabatic pentru fiecare experienta efectuata. Se calculeaza
valoarea medie facand media aritmetica a valorilor obtinute.
Luand D h1=D2=D
h, relatia de calcul a erorii relative este:
![]() (13)
(13)
Inmultind valoarea determinata, cu eroarea relativa se obtine
eroarea absoluta D?m.
Rezultatele se trec in tabelul 1.
Tabelul 1
| h1 (cm) | h2 (cm) | g | D h (cm) | Dg /g (%) | gm±g |