A METALELOR

Consideratii teoretice

Curentul electric este o miscare dirijata de sarcini electrice ca urmare a aplicarii unui camp electric. Aceasta miscare ordonata se suprapune peste miscarea haotica de agitatie termica. La metale, purtatorii de sarcina ce formeaza curentul de conductie sunt electronii din banda de valenta partial ocupata. Ei creeaza intr-o portiune din interiorul conductorului de sectiune D S, prin care trece sarcina D Q in timpul D t, densitatea de curent "j" a carei marime este:

j=D Q/(D S·D t) [j]_SI =A/m² (1)

iar sensul dat de sensul de deplasare al sarcinilor pozitive in campul E. Pe de alta parte D Q este sarcina cuprinsa in volumul D V = D S·v_d·D t si este data de relatia :

D Q = n·e·v_d·D S·D t (2)

unde:

• v_d – este viteza medie de transport a electronilor in conductor sub actiunea campului E, numita viteza de drift sau antrenare;
• n·e – densitatea de sarcina electrica din interiorul conductorului (e=1,6·10^–19C).

Viteza de drift este mai mica decat viteza de agitatie termica si este imprimata electronilor de campul electric E in timpul ? – timpul mediu dintre 2 ciocniri. Conform legii a doua a lui Newton, acceleratia imprimata electronului de catre campul electric E este:

Atunci viteza maxima atinsa de electron inainte de urmatoarea ciocnire este:

iar viteza medie a miscarii ordonate (viteza de drift sau transport) va fi:

Coeficientul de proportionalitate poarta denumirea de mobilitate a purtatorilor:

Tinand seama de cele de mai sus, densitatea de curent poate fi exprimata astfel:

si poarta numele de forma diferentiala a legii lui Ohm. Constanta de proportionalitate "s " reprezinta conductivitatea electrica si este data de relatia:

Considerand densitatea de curent uniform distribuita in interiorul unui conductor de sectiune S si lungime l obtinem din relatia (6):

forma finala a legii lui Ohm. La conductorii cu sectiune constanta rezistenta electrica se exprima simplu:

unde r = l/s – rezistivitatea electrica, caracterizeaza capacitatea unei substante de a conduce curentul electric [r ]_SI = W ·m.

Rezistivitatea unui metal continand atomi de impuritate are forma:

unde r_L este rezistivitatea produsa de agitatia termica a ionilor din nodurile retelei cristaline a metalului, iar r_i este rezistivitatea cauzata de imprastierea undelor asociate electronilor pe atomii de impuritate ce perturba periodicitatea retelei.

Valoarea rezistivitatii este determinata de natura substantei si de conditiile in care se afla ea. Pentru majoritatea metalelor, la temperaturi indepartate de zero absolut, rezistivitatea creste cu temperatura aproximativ dupa legea liniara:

si defineste un coeficient termic mediu al rezistivitatii:

unde T₀ = 273,16 °K. Acest coeficient este egal cu ~1/273 la majoritatea metalelor pure.

Metoda experimentala

Instalatia experimentala

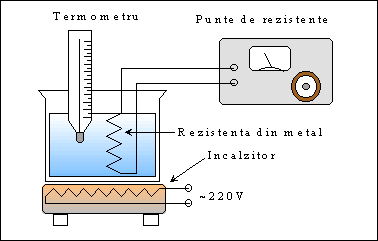
Schema de principiu a instalatiei este prezentata in figura 1. Instalatia contine o rezistenta bobinata din cupru, sarma de f 0,1 mm, introdusa intr-un vas termorezistent cu ulei, asezat pe plita unui resou electric. Rezistenta se masoara cu o punte INEB, avand clasa de precizie g =10 ^–2. Pentru masurarea temperaturii se foloseste un termometru cu mercur.

Figura 1. Instalatia experimentala.

Mod de lucru

1. Se masoara cu ohmmetrul rezistenta electrica a firului metalic la temperatura camerei.
2. Se conecteaza plita la reteaua electrica si se urmareste cresterea rezistentei cu cresterea temperaturii. Citim temperatura din 5 in 5 ^oC si valorile corespunzatoare ale rezistentei, trecandu-le in tabelul 1.
3. Se calculeaza rezistivitatea tinand cont ca sarma de cupru bobinata pe carcasa are lungimea ?=65m si f =0,12mm (pentru rezistenta din platina ?=1,85m si f =0,05mm); r = R·S/? = R·[p ·f²/(4·?)]
4. Se calculeaza conductibilitatea ? = l/rpentru temperaturile la care s-au facut citirile de rezistenta.
5. Se calculeaza mobilitatea m= ?/(n·e). Pentru cupru concentratia electronilor de conductie fiind de un electron pentru un atom si A=63 kg / kmol, d = 8900 kg /m? si N_A = 6,023·10²⁶ atomi /kmol, putem scrie: n = d·N_A/A (la Pt A=195 kg/kmol, d =21450 kg /m?)
6. Se reprezinta pe acelasi grafic r = r (t) si m = m (t).
7. Din panta graficului se determina coeficientul de temperatura al rezistivitatii cuprului, a , utilizand relatia (12) sau R₁=R_o·(1+a ·t₁) si R₂=R_o·(1+a ·t₂) de unde avem a =(R₁–R₂)/(R₂·t₁–R₁·t₂).
8. Se calculeaza durata drumului liber ? =m·m/e la t_camera.
9. Rezultatele se trec in tabelul 1.

Calculul erorii se face cu relatia: