DETERMINAREA

CONSTANTELOR LUI STEFAN–BOLTZMANN SI PLANCK CU AJUTORUL RADIATIEI TERMICE

Consideratii teoretice

Radiatia termica este alcatuita din undele electromagnetice emise de orice corp cald (T>0K). Fluxul de radiatie nu este monocromatic ci este alcatuit din componente cu diferite frecvente (sau lungimi de unda). Fluxul energetic integral este cantitatea de energie radiata in unitatea de timp:

F = dW/dt [F ]SI =W

Radianta energetica integrala = fluxul energetic integral raportat la aria suprafetei care radiaza:

R=dF /dS [R]SI = W/m2

Fluxul energetic spectral este fluxul energetic pentru intervalul de frevente (sau lungimi de unda) [n ,n +dn ] sau [l , l +dl ]:

Fl =dW/dl [Fl ]SI = W/m


Radianta spectrala =radianta corespunzatoare intervalelor [n ,n +dn ] sau [l ,l +dl ]:

rl = dR/dl [rl ]SI = W/m3

astfel ca
Aceasta marime se numeste si "putere de emisie spectrala".

Legile radiatiei termice au fost deduse pentru "corpul absolut negru" in conditii de echilibru termodinamic. "Corpul absolut negru" este acel corp care are o putere de absorbtie egala cu unitatea. Se numeste putere de absorbtie raportul dintre fluxul absorbit (Fa) si fluxul incident (Fi) pe suprafata corpului:

A=Fa /Fi (integral) sau

Al = Fal/Fil(spectral)

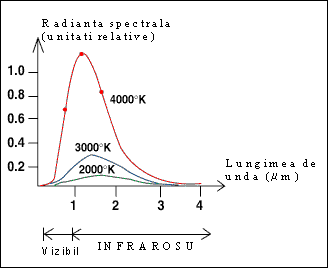Figura 1. Radianta spectrala

I. Legea lui Kirchhoff. Raportul dintre puterea de emisie spectrala si puterea de absorbtie spectrala depinde numai de l si T, dar nu depinde de natura corpului:

rl /Al = f(l ,T)

Pentru corpul absolut negru avem : Al = 1 sau 100% astfel ca:

rl = f(l ,T).

Gasirea formei functiei f(l ,T) este problema fundamentala a teoriei radiatiei termice.

II. Legea lui Stefan si Boltzmann. Radianta integrala a corpului absolut negru este proportionala cu T4:

R = s ·T4

unde s = 5,67·10– 8 W/(m2·K4) este constanta lui Stefan-Boltzmann

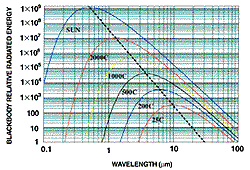
III. Legea lui Planck a radiatiei termice spune ca distributia energiei radiatiei termice, in functie de lungimea de unda (sau de frecventa) este de forma:

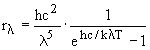
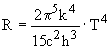unde h = 6,62·10– 34 J·s, constanta lui Planck (sau constanta "actiunii"), c @ 300.000 km/s este viteza luminii in vid, iar k =1,38·10–23 J/grad este constanta lui Boltzmann. Cu legea lui Planck se demonstreaza ca:

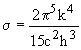deci  si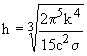 

Corpurile care radiaza termic nu sunt corpuri absolut negre, ele avand o putere de absorbtie si implicit de emisie mai mica decat unitatea.

Un corp cu temperatura T1 radiaza prin suprafata de arie "S" in timp de o secunda, energia:

W1 = s ·S·T14

Din partea mediului ambiant cu temperatura T2 corpul primeste si absoarbe, pe aceeasi arie S, tot intr-o secunda energia:

W2 = s ·S·T24

Energia neta radiata de acest corp intr-o secunda este deci:

W = W1 – W2= s ·S·(T14 – T24)         (1)

Deoarece corpurile noastre nu sunt absolut negre, ci "gri", trebuie sa mai introducem o constanta experimentala B emisivitatea, asa ca (1) devine:

Wexp = B·S·s ·(T14 – T24) (2)

Metoda experimentala

Corpul cald este o platbanda din Kantal ce poate fi incalzita pana la incandescenta, trecand prin ea un curent electric de intensitate I . Puterea electrica absorbita de platbanda este:

P=I·U         [P]SI =W         (3)

unde: I este intensitatea curentului electric (A), iar
        U este caderea de tensiune pe platbanda, intre contacte (V).

Cand temperatura platbandei este constanta (echilibru termic) avem egalitate intre puterea primita (aici putere electrica) si puterea pierduta (prin radiatie in special la temperaturi mari, peste 600oC), de unde avem:

Wexp = P (2·?·d) B·s ·(T14 – T24)= U·I (4)

iar constanta lui Stefan si Boltzmann este:

s =I·U / [2·l·d·B·(T14 – T24)]         [W/(m2·K4]             (5)

unde:     T2 este temperatura mediului ambiant,
            T1 este temperatura platbandei,
            l este lungimea benzii (intre contactele electrice),
            d este latimea ei.

Se ia de doua ori produsul "l·d" deoarece banda are doua fete libere (daca in loc de platbanda se foloseste o bara cilindrica, sau de alta sectiune, se exprima suprafata radianta in mod corespunzator).

Mod de lucru

  1. Se masoara lungimea l si latimea d a platbandei (cu rigla, subler).
  2. Crestem tensiunea electrica de alimentare pana cand platbanda devine incandescenta (culoare rosie).
  3. Se determina tensiunea "U" si curentul "I" al benzii incalzite.
  4. Temperatura T1 a platbandei se masoara cu un pirometru cu disparitie de filament.
  5. Temperatura T2 a mediului se masoara cu un termometru obisnuit.
  6. Datele experimentale se trec in tabel.
Prelucrarea datelor experimentale

1. Se calculeaza aria radianta a platbandei S= l·d.

2. Din relatia (5) se obtine valoarea lui s (B = 0,96).

3. Se face media aritmetica smediu=(s1+s2+s3)/3. Se exprima valoarea probabila a lui s s =smediu ±Ds [W/(m2·K4]

4. Se calculeaza constanta lui Planck din relatia:

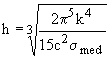(6)

5. Se face schita instalatiei experimentale.

Tabelul A
Nr. crt. l
(m)		 d 
(m)		 I
(A)		 U
(V)		 T1
(K)		 T2
(K)		 s
[W/(m2·K4]		 h
[J·s]
1.                
2.                
3.