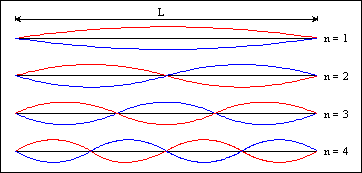
Figura 1. Moduri de vibratie intr-o coarda de lungime L.
I. Considerente teoretice
Undele transversale (particulele mediului oscileaza perpendicular pe directia de propagere) sunt posibile numai in mediile solide elastice. In cazul corzilor (fire elastice cu sectiune constanta) viteza frontului de unda in coarda supusa unei tensiuni mecanice T si avind o densitate liniara m = m/L este:
v = (T/m )1/2 (1)
In coarda se propaga in sens direct unde progresive, iar in sens invers unde regresive. Pentru oscilatii armonice, functiile de unda care descriu propagarea undei progresive si a undei regresive sunt:
f1(t–x/v) = A·sin [w ·(t–x/v)] = A·sin(w ·t–k·x)
f2(t+x/v) = A·sin [w ·(t+x/v)+p ] = A·sin(w ·t+k·x+p ) (2)
unde k=w /v=2p /l este numarul de unda. Interferenta acestor unde va da nastere in coarda unor unde numite unde stationare descrise de ecuatia:
F=f1+f2 =2·A·cos(k·x+p /2)·sin(w ·t+p /2) =2·A·sin(k·x)·cos(w ·t) (3)
Aceasta ecuatie reprezinta ecuatia undelor stationare sau a modurilor de vibratie intr-o coarda. Conform acestei ecuatii fiecare punct al mediului executa o oscilatie de amplitudine constanta in timp, dar distribuita in spatiu dupa relatia A(x) = 2·A·sin(k·x). Valorile minime ale amplitudinii se obtin in anumite puncte numite noduri, care satisfac conditia:
A(x)=0, adica k·x = n·p
de unde se obtine:
xnod = n·p /k = n·p /[2p /l ] = n·l /2 n = 1,2,3,… (4)
Valorile de amplitudine maxima, numite ventre, satisfac conditia:
A(x)= ± 2·A, adica k·x=(2n+1)p /2
sau xventru = (2n+1) l /4 n = 1,2,3,… (5)
Energia undelor stationare ramine localizata, neputindu-se transmite, teoretic, prin noduri.
La capete, deoarece coarda este fixa, vor exista noduri, iar lungimea corzii si lungimea de unda l vor fi legate prin relatia de discretizare (cuantificare) a luiTaylor:
L = n·ln /2 ln=2·L/n n = 1,2,3,… (6)

Figura 1. Moduri de vibratie intr-o coarda
de lungime L.
Tinind cont de viteza undelor transmise prin coarda, rezulta ca undele stationare, sau modurile de vibratie ale corzii, pot avea numai anumite frecvente, cuantificate prin relatia:
nn = v/ln = (n/2L)(T/m )1/2 n = 1,2,3,… (7)
Pentru n=1 se obtine frecventa fundamentala, n1, careia ii corespunde modul fundamental de vibratie (armonica fundamentala) iar pentru celelalte valori ale lui n se obtin armonicele superioare. Frecventele pentru care coarda vibreaza in regim stationar alcatuiesc un spectru discret de valori proprii de vibratie al corzii, sau rezonantele. Acestea impreuna formeaza modurile de vibratie ale corzii si sunt ilustrate in figura 1.
II. Metoda experimentala
Dispozitivul experimental prezentat in figura este format dintr-un suport pe care este intins un fir metalic avind un capat fixat, iar celalalt trecut peste un scripete fix. De acest capat se atirna diferite greutati G, pentru a se tensiona (intinde) in mod diferit coarda (T = G).
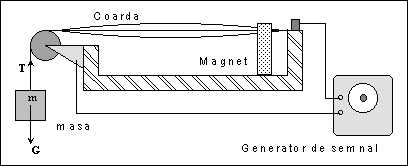
Figura 1. Montajul experimental.
Prin fir trece un curent electric de audiofrecventa provenit de la un generator de semnal care permite reglarea frecventei si a nivelului curentului. Interactiunea dintre curentul ce trece prin fir si cimpul magnetic constant produs de magnetul permanent genereaza o forta (F=B·I·?) ce pune in vibratie coarda.
Modul de lucru
1. Se calculeaza viteza de propagare a undelor transversale prin coarda folosind relatia (1) sau mai explicit:
vteor = (T/m ) = (2/d)·[m·g/(p ·r )]1/2 (8)
unde: r = 8900kg/m3
densitatea cuprului;
d = 0,28 mm diametrul firului de cupru;
L = 0,625 m lungimea corzii.
2. Se determina lungimile de unda corespunzatoare diferitelor moduri de vibratie cu ajutorul relatiei:
ln =2·L/n (9)
si viteza de propagare a undei transversale cu relatia :
vexp = ln·nn (10)
unde nn este frecventa corespunzatoare modului de vibratie n.
Formulele pentru calculul erorilor sunt:
D ve /ve = D L/L+Dn /n D vt /vt = D d/d+(D m/m+D g/g+Dr /r )/2
Datele si rezultatele se trec in tabelul de mai jos.
Tabelul A
| m
(kg) |
L
(m) |
d
(m) |
r
(kg/m3) |
vt
(m/s) |
n | ln
(m) |
nn
(Hz) |
vexp
(m/s) |
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 |