ACUSTICA

6. Timpul de raspuns al unui termocuplu

Timpul de raspuns al unui termocuplu reprezinta timpul necesar termocuplului pentru a ajunge la temperatura mediului masurat. Ca sa se incalzeasca termocuplul preia prin conductie termica caldura de la mediul monitorizat. Rezistentele termice corespunzatoare mediilor traversate de fluxul termic de la mediul masurat pana la jonctiunea termocuplului se insumeaza.

Procesul poate fi descris fizic prin intermediul unei ecuatii de bilant termic :

caldura primita prin conductie termica de la mediul masurat =

= caldura acumulata in termocuplu + caldura pierduta prin conductie termica catre mediul exterior .

Concret, neglijand pierderile, avem :

caldura acumulata de termocuplu

dQ = m·c·dT = H·dT

caldura cedata de mediul masurat

dQ = (l ·S/L)·(T_m–T)·dt = G·(T_m–T)·dt

Ecuatia de bilant termic este: G·(T_m–T) = H·dT/dt (24)

Rezolvand-o prin separarea variabilelor :

(G/H)·dt = dT/(T_m–T)

=> dt/t = dT/(T_m–T), t = H/G

=> t/t = - ln[(T_m–T)/(T_m–T₀)] (25)

se obtine legea de variatie a temperaturii dupa timp:

T(t) = T_m– (T_m–T₀ ) · e-^{t / t}

Timpul de raspuns, t = H/G, este direct proportional cu capacitatea termica a termocuplului H si rezistenta termica termocuplu-mediu 1/G (invers proportional cu conductanta termica mediu-termocuplu, G).

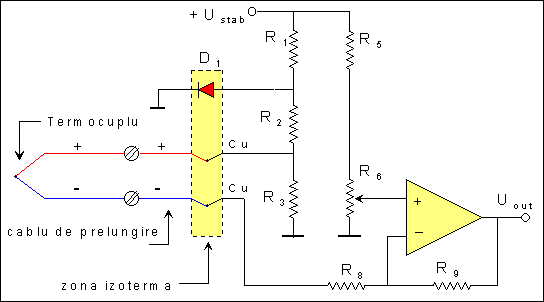
7. Circuit electronic pentru termocuplu [5]

Un amplificator operational de precizie preia diferential semnalul de la termocuplu si o punte in care se afla o dioda cu rolul de compensare a jonctiunii reci.
Rezistenta R₁ injecteaza curent in dioda de siliciu D.
Coeficientul de temperatura al tensiunii de deschidere al diodei fiind - 2,1 mV/^oC, este divizat prin intermediul rezistentelor R₂ si R₃ pentru a ajunge la valoarea de 40,7 m V/^oC corespunzatoare coeficientului Seebeck al termocuplului de tip K (cromel-alumel).
Prin intermediul potentiometrului R₆ de la intrarea "+" a amplificatorului operational se realizeaza aducerea la zero a iesirii acestuia cand jonctiunea de masurare a termocuplului este la 0 ^oC.
Rezistentele R₈ si R₉ stabilesc amplificarea circuitului :

A = R₉ /R₈ = 10 mV/0,0407 mV = 245,7

astfel incat sa avem la iesirea amplificatorului operational 10 mV/^oC, ceea ce permite o citire usoara a temperaturii folosind ca dispozitiv de afisare un voltmetru digital.

Bibliografie

B. Yavorski, A. Deltaf, "Aide-memoire de physique", Ed. Moscou 1975.
H.G. Mitchell, "A textbook of electricity", Ed. M.K.S. 1960.
I. Asavinei, C. Niculescu, "Ghid pentru utilizarea termocuplelor in masurari industriale", Editura Tehnica 1981.
Catalog Driver-Harris 1990, pag. 110
S. Sokolov, J. Wong, Electronic Design 1 oct. 1992, pag 53