Research fields
The research activity of the CERTETA team is mainly focused on the following fields:
Analysis of sheet metal formability
The forming limit diagrams (FLD) method has been used in order to assess the formability of sheet metals. The modelling of the FLD's has been carried out using the Marciniak-Kuczinsky and Hutchinson-Neale models. Experimental investigations have also been carried out, using the facilities available in the CERTETA laboratory. An important factor influencing the formability that has been studied is the pulsatory loading. It has been shown experimentally and theoretically that an incremental loading improves the sheet formability.
Several anisotropic yield criteria (Hill 1948, 1979 and 1993, Cazacu-Barlat 2001, BBC2000, BBC2005 and BBC2008) have been implemented in the theoretical models of FLD (see Figure 1).
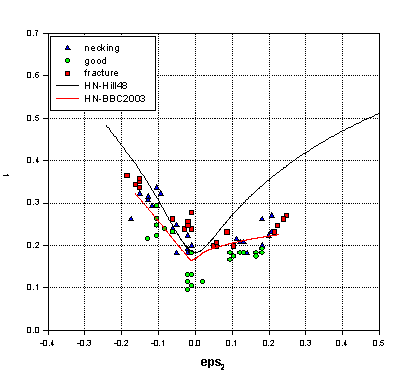
Figure 1. FLDs calculated using different yield criteria for AA6181-T3 aluminium alloy
A new strategy for calculating Forming Limit Diagrams using the finite element method has been developed. The simulations have been performed with Abaqus/Standard. The constitutive model (BBC2005) has been implemented using a UMAT subroutine. The comparison with the experimental values proves the capability of the finite element method to predict correctly the strain localization.
A computer programme used for interactive calculation of Forming Limit Diagrams (FORM-CERT) has been developed. The programme is based on a Hutchinson-Neale model. Different yield criteria (Hill 1948, Barlat-Lian and BBC 2005) are implemented in this model. The programme consists in three modules: a graphical interface for input, a module for the identification and visualization of the yield surfaces, and a module for calculating and visualizing the forming limit curves. A useful facility offered by the programme is the possibility to perform the sensitivity analysis both for the yield surface and the forming limit curves (see Figure 2). The numerical results can be compared with experimental data, using the import/export facilities included in the programme. The programme may be incorporated in finite element codes.
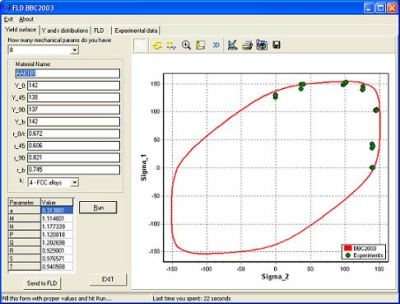
Figure 2.a
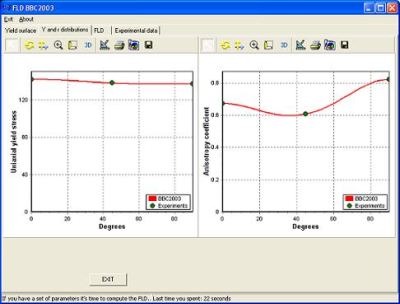
Figure 2.b
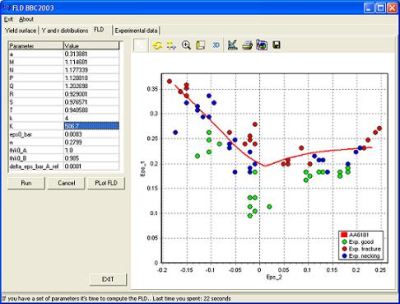
Figure 2.c
Figure 2. User-friendly interface of the programme used to calculate the yield locus (Figure 2.a), distribution of the uniaxial yield stress, anisotropy coefficient (Figure 2.b) and the Forming Limit Curve (Figure 2.c) for AA6181 aluminum alloy.
Theoretical and experimental research on anisotropic behaviour of sheet metals
This project has been developed in cooperation with the Institute of Metal Forming (IFU) - University of Stuttgart. It deals with the yielding phenomena of different metallic sheets, especially aluminium. Complex experiments for the determination of the yielding curves have been carried out. Several anisotropic yield criteria have been proposed in order to describe the behaviour of the sheet metals ( BBC2000 and BBC2003) (see Figure 3). A version of the BBC 2005 model (BBC 2005 ) has been implemented in the AUTOFORM 4.1 Finite Elemente commercial program. Recentlly, some new models have been proposed (Comsa-Banabic 2007 and BBC 2008 ).
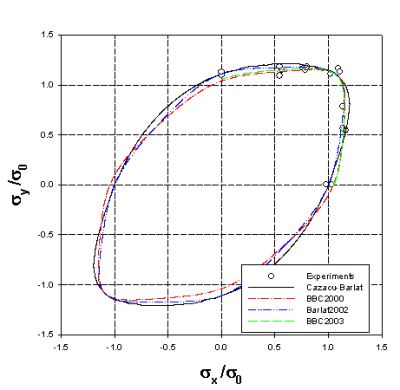
Figure 3. Yield locus calculated using different yield criteria vs. experimental points for AA3103-0 aluminium alloy
Deep-drawing optimization by controlling the blank-holding force
Several mathematical models have been developed in order to establish the variation of blank-holding forces, using as criteria the avoidance of flange thickening and the minimisation of the forming energy. The laboratory has two deep-drawing devices allowing the control of the blank-holding force through a computer.
Superplasticity
The research deals with the formability of the superplastic materials using the FLD's method. An analytical model has been developed to determine the pressure-time relationship in order to keep a constant strain rate during the bulge process. Pulsatory loading on the formability of superplastic materials has been studied.
Finite element simulation of deep-drawing, stretching and hydrostatic bulging processes
Several computer programmes have been developed for the simulation of sheet-metal forming processes. Both elasto-plastic and rigid-plastic material models have been used. Several yield criteria (Hill 1990, Barlat-Lian, BBC2000 , BBC 2005 , BBC 2008 and Comsa-Banabic 2007 ) have been implemented in ABAQUS, LS-Dyna and AUTOFORM 4.1 programs for simulating the different sheet metal forming processes. The numerical results have been compared with experimental data (see for exemple, Figure 4). The comparison aims to evaluate the performances of the yield criteria mentioned above: accuracy of the predictions and numerical efficiency of the mechanical models (convergence rate, speed of the computation, etc.).
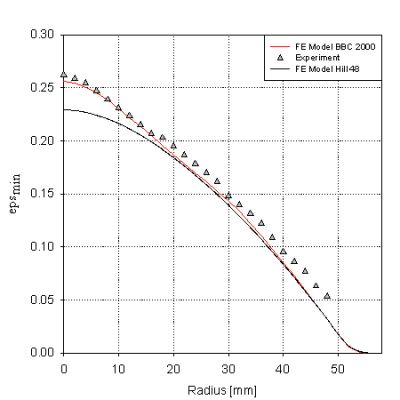
Figure 4. Predicted and experimental minor strain in bulge forming for AA3103-0 aluminum alloy
